通常情况下，岩石中的裂隙可视为由于应力作用产生的定向排列的二维线形饱和流体的散射体（图1）。地震波在传播过程中，慢纵波与散射体相互作用，产生地震波速度频散以及能量衰减，进而作为识别裂隙的重要信息。目前速度频散及衰减曲线常基于三维裂隙理论，结合分支函数（branching function），通过插值手段得到。但是这种插值手段作为一种半经验方法，未能揭示地震波与裂隙作用的本质，其准确性受到质疑，需要从基本动力学方程出发，分别讨论不同频率范围下地震波与裂隙的相互作用方式，进而建立精确的描述二维裂隙速度频散以及能量衰减特征的模型。

图1 岩石中二维裂隙分布状态示意图：黑色椭圆形包含物为裂隙，其背景介质为孔隙弹性介质 

　　针对上述问题，我室博士生付博烨与导师符力耘研究员等，首次从孔隙弹性方程出发，将背景介质中的二维裂隙视为一阶扰动，解决了孔隙弹性方程的混合边值问题，从而计算了裂隙产生的地震速度频散以及能量衰减，揭示出地震波与裂隙作用的本质（图2），相比于其他方法，该方法更严格，结果可信度更高。

　　研究还取得了以下认识：(1) 当慢纵波波长与裂隙尺度近似时，速度频散与能量衰减强度最大，说明慢纵波是诱发速度频散和能量衰减的主要原因。当地震波发生的能量衰减最强时，根据慢纵波波长可推测裂隙平均长度。 (2) 当频率较低时，地震波速度最小，此时慢纵波波长最长，导致裂隙内部流体与背景介质之间充分相互作用，产生强烈粘滞耗散，使得速度降低；反之亦然。（3）从理论上证明了分支函数插值的简单性与准确性，为其广泛应用提供了基本依据。

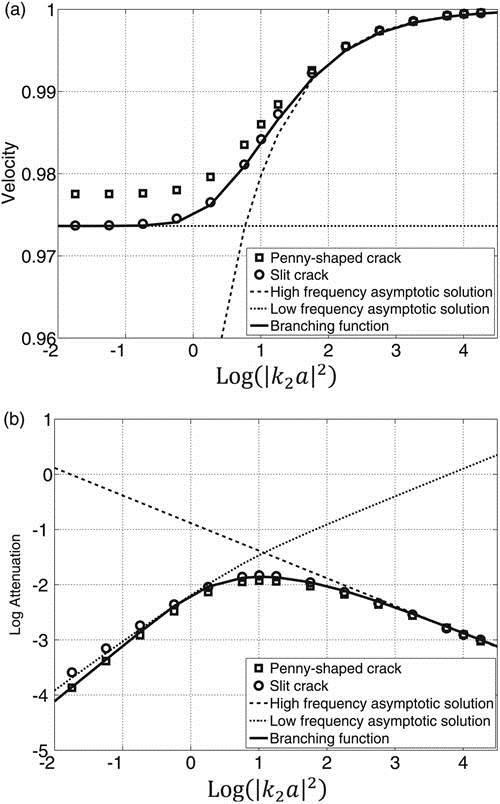
图2 不同模型计算值对比（a）速度频散对比；（b）能量衰减对比 

　　研究成果发表于Journal of Geophysical Research: Solid Earth。（Fu B Y, Guo J, Fu L Y, et al. Seismic dispersion and attenuation in saturated porous rock with aligned slit cracks[J]. Journal of Geophysical Research: Solid Earth, 2018, 123(8): 6890-6910.）（原文链接）